Synthèse d'un son

En 1957, Max Mathews réalise aux USA le premier enregistrement numérique et la première synthèse de sons par ordinateur. Depuis, les méthodes de synthèse se sont multipliées et améliorées. En voici quatre, parmi les plus répandues et intéressantes :

La synthèse additive :

C'est une forme de synthèse très simple sur le principe. Elle consiste à superposer une sinusoïde correspondant à une fondamentale, et ses harmoniques. C'est cette forme de synthèse que nous avons retenue et choisi de mettre en oeuvre dans notre TPE.

La synthèse soustractive :

Simple également dans le principe, elle est beaucoup plus compliquée à mettre en œuvre, car elle consiste à prendre une onde de départ très riche en harmoniques (une onde carrée dans l'idéal, car elle est composée d'une infinité de fonctions sinus) et d'enlever les harmoniques inutiles à l'aide d'une série de filtres dits “passe–bas”, c'est à dire capables d'isoler et de séparer certaines plages de fréquences, donc certains harmoniques.

La synthèse granulaire :

C'est une forme de synthèse bien plus complexe. Elle est fondée sur les mêmes idées que celle de Fermat lorsqu'il a étudié la lumière et l'énergie considérées comme des fluides continus : découper l'onde sonore en “grains” comme on décompose l'énergie en quanta ou la lumière en photons. Elle consiste à ajouter des “grains” sonores afin de reconstituer l'instrument. Elle est donc très compliquée, très fastidieuse, mais elle permet de synthétiser tous les sons sans distinction (voix humaines comprises) et donne des résultats exceptionnels.

La synthèse par modèles physiques :

C'est la plus intéressante des formes mais aussi la plus compliquée, et donc peu utilisée. Elle consiste à modéliser l'intégralité d'un instrument et étudier la façon dont il résonnerait. On créé ainsi des violons virtuels, des guitares virtuelles mais aussi des instruments qui n'existent pas !

a) Transformée de Fourier

Pour l'instant, nous avons un petit problème : en effet, le signal obtenu à l'aide d'un microphone n'est qu'une longue courbe inexploitable telle quelle. Pour en extraire les informations qui nous intéressent, il existe heureusement un outil extrêmement puissant : la transformée de Fourier, que nous avons rapidement évoquée. Il s'agit d'une opération mathématique permettant d’associer à une fonction "quasi-périodique" son spectre en fréquences, c’est-à-dire de donner les coefficients des sinus qui sont additionnés pour donner la courbe finale.
Pourquoi "quasi-périodique" ? En fait, la périodicité parfaite du son n'est que théorique. En pratique, le motif "périodique" varie légèrement, c'est pourquoi le son évolue au cours du temps (voir l'enveloppe ADSR).

Le logiciel Foxy permet de réaliser cette fameuse transformée de Fourier : à une portion de sinusoïde, il associe un spectre en fréquences. Ainsi on voit que la fondamentale H1 a bien pour fréquence 440Hz, puis viennent les harmoniques H2, H3, h3...

b) Partiels

Cependant un son "parfait" composé uniquement des harmoniques de la fondamentale n'existe que théoriquement. En pratique, une source sonore émet également des fréquences qui ne sont pas des multiples entiers de la fondamentale : on ne parle plus d'harmoniques mais de partiels. Ainsi le partiel 4,2 d'une fondamentale de 100Hz a pour fréquence 420Hz. Plus exactement, les harmoniques sont les cas particuliers des partiels.

Un instrument de musique émet donc en fait dans presque toutes les fréquences, avec des intensités bien plus importantes pour les partiels dont les fréquences se rapprochent de celles des harmoniques de l’instrument. On peut le vérifier par une expérience très simple : en soufflant plus ou moins fort dans un bambou, le son émis est plus ou moins aigu, mais reste quand même très proche de la fréquence de résonance du bambou, laquelle dépend de ses qualités intrinsèques et ne change donc pas.

Voici donc à quoi ressemble un "vrai" spectre sonore (en rouge), donné par le logiciel Goldwave. En abscisse, on a la fréquence (en Hz, échelle logarithmique), en ordonnée, l'intensité de chacune de ces fréquences par rapport à une valeur référence (en déciBel) :
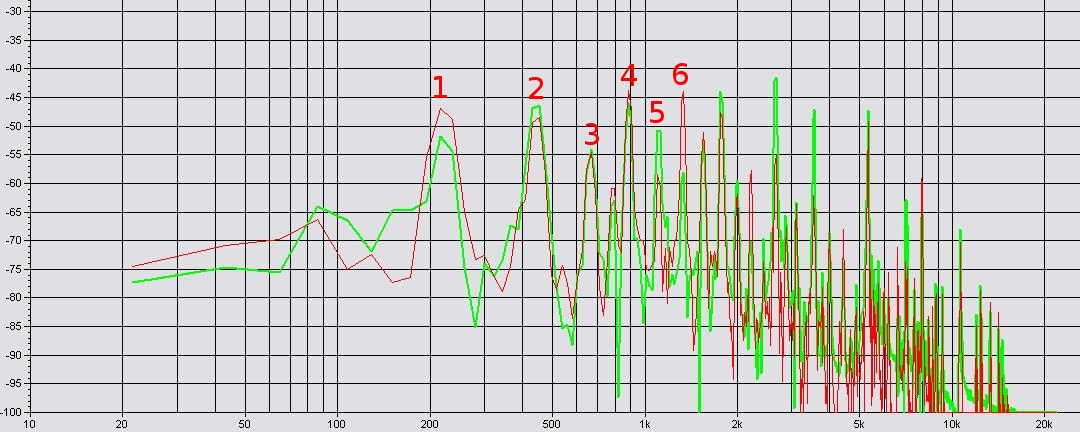
Ainsi, on constate un premier "pic" autour de 220 Hz : c'est donc la fondamentale de notre son. Puis un autour de 440Hz, de 660Hz, de 880Hz... Ce sont, bien sûr, les premiers harmoniques.

Calculer leur fréquence est facile ; pour leur intensité, c'est à peine plus difficile : Sur le graphique, la fondamentale f₁ a pour intensité -47 dB par rapport à une valeur référence (dont la valeur en W·m^-2 n'a pas d'importance). Ainsi :

10·log( I₁ / I₀ ) = -47
<=> log( I₁ / I₀ ) = -4.7
<=> I₁ / I₀ = 10^-4,7
<=> I₁ / I₀ ~ 1/50 000

Donc l'intensité en W·m^-2 de f₁ est 50 000 fois plus faible que I₀ . Prendre cette valeur I₀ comme référence n'est donc pas très pratique. Mais, puisque le dB est justement une unité comparative de deux valeurs, on peut prendre I₁ comme référence !

Tableau intensités — Intensités des harmoniques par rapport à I₁

Ainsi, on voit que l'harmonique 3 a une intensité environ 6 fois plus faible que la fondamentale, et qu'en revanche l'harmonique 4 est 2,5 fois plus fort. Le fréquence perçue par l'oreille aura donc la fréquence de cet harmonique 4 dominant : 4 x 220Hz = 880Hz

c) Synthèse

Nous avons enfin tous les éléments en main pour passer à la synthèse informatique d'un son. Pour cela, nous utiliserons le logiciel Csound, programmé à partir du langage C, et qui permet de réaliser des synthèses sonores extrêmement complexes. Nous n'en emploierons cependant que des fonctionnalités basiques : superposition de signaux sinusoïdaux de fréquence et d'amplitude variables, et définition d'une enveloppe pour chacun de ces signaux.

Pour ce TPE, nous allons reproduire le début du Toccata et Fugue en Ré mineur pour orgue de Jean-Sébastien Bach :

Transformée de Fourier

Pour obtenir notre spectre en fréquences, il faut appliquer la transformée de Fourier sur une portion ni trop grande ni trop petite du son : si celle-ci est trop courte, le spectre souffre d'un manque de précision, si elle est trop longue, le spectre représente une moyenne des différentes phases du son, qui ne sont pas mélangeables.

Orgue GoldWave — Sur cette image, on a représenté l'ensemble de la première note. En pratique, la sélection doit être bien plus courte. Il y a deux courbes car le fichier audio de base est en stéréo

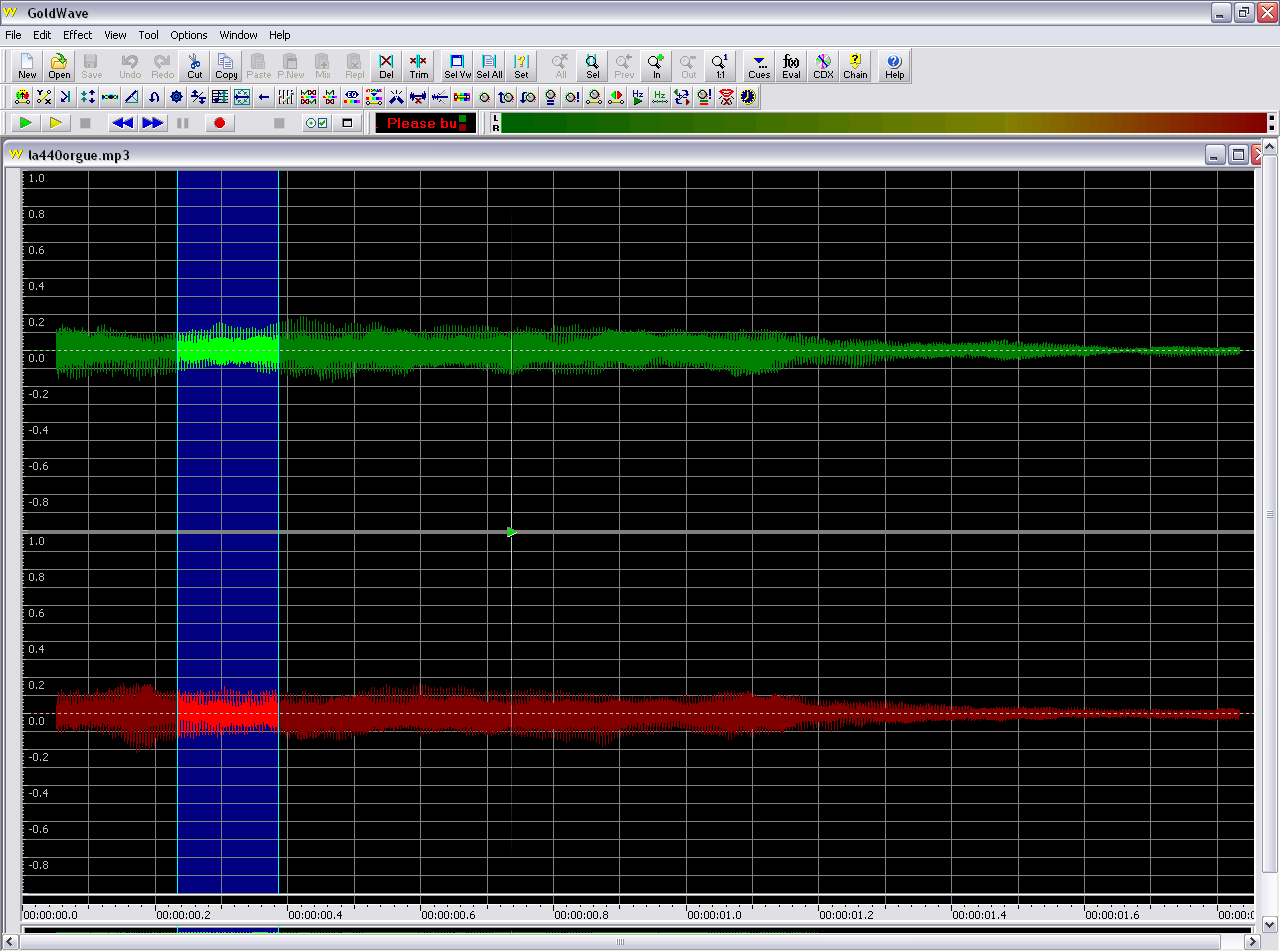
Première partie du son

La transformée de Fourier appliquée au début du son nous révèle le spectre de fréquences ci-dessous. La fondamentale a pour fréquence 220Hz (La2), et l'harmonique dominant est l'harmonique de rang 4 (880Hz, c'est un La4) :

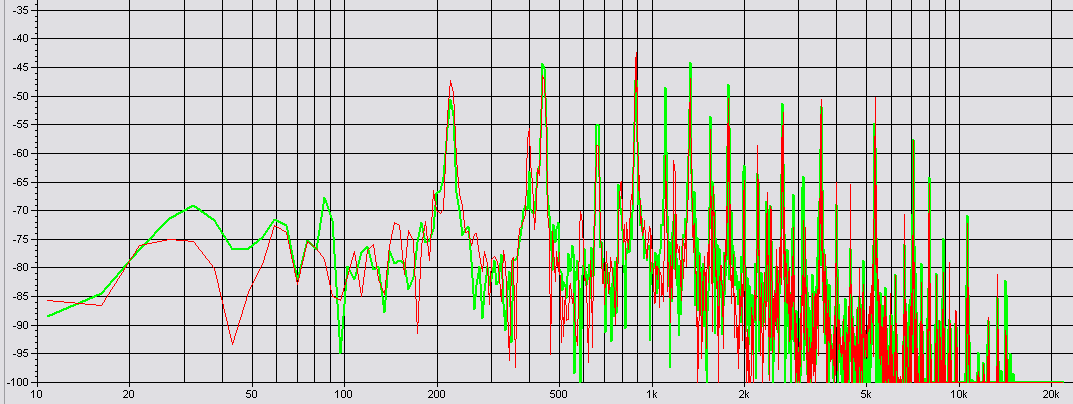
Transposé dans un tableur, ce spectre nous donne les amplitudes qu'il faudra appliquer aux harmoniques lors de la synthèse. Quel est le rôle de la dernière colonne ? Dans Csound, l'amplitude maximale que l'on peut appliquer à un signal est 32 767. Multiplier par 32 767 les intensités relatives à I4 (comprises entre 0 et 1) permet donc d'obtenir la précision maximale :

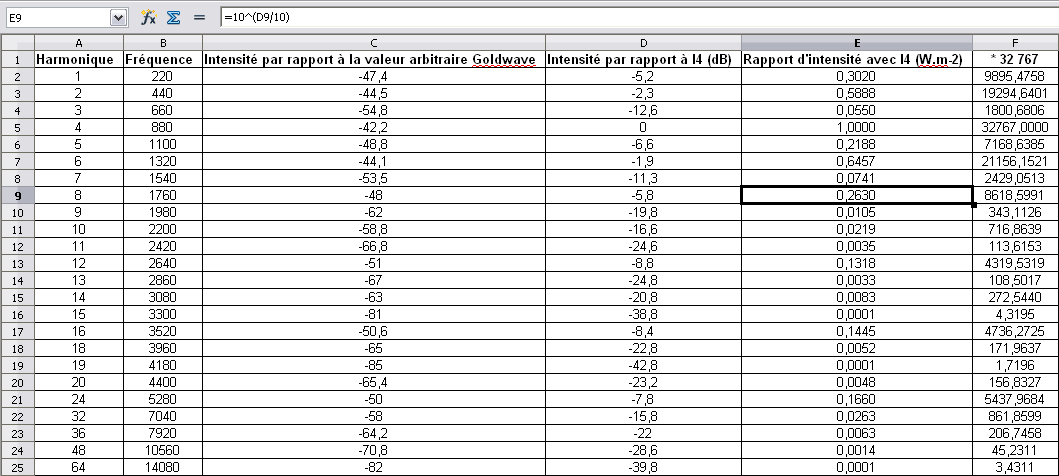
Deuxième partie du son

Une deuxième transformée de Fourier appliquée à la fin du signal nous donne cet autre spectre :

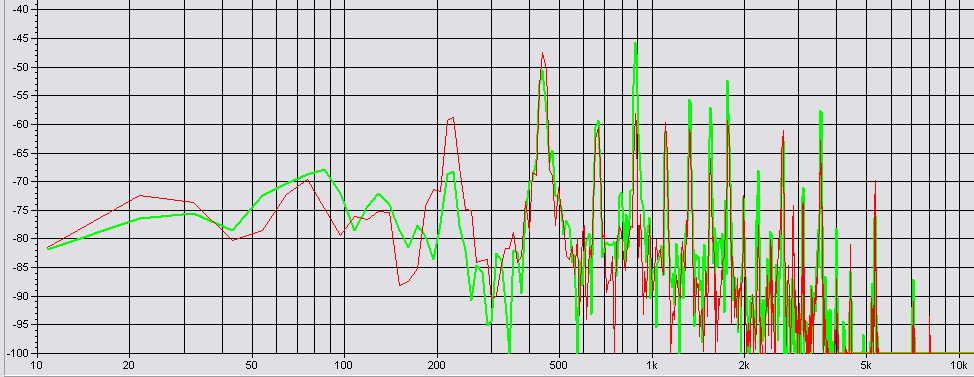
On constate notamment que les harmoniques de fréquence supérieure à 5 000Hz ont presque disparu.

Synthèse

Enfin, on rentre les données récoltées dans le logiciel Csound :

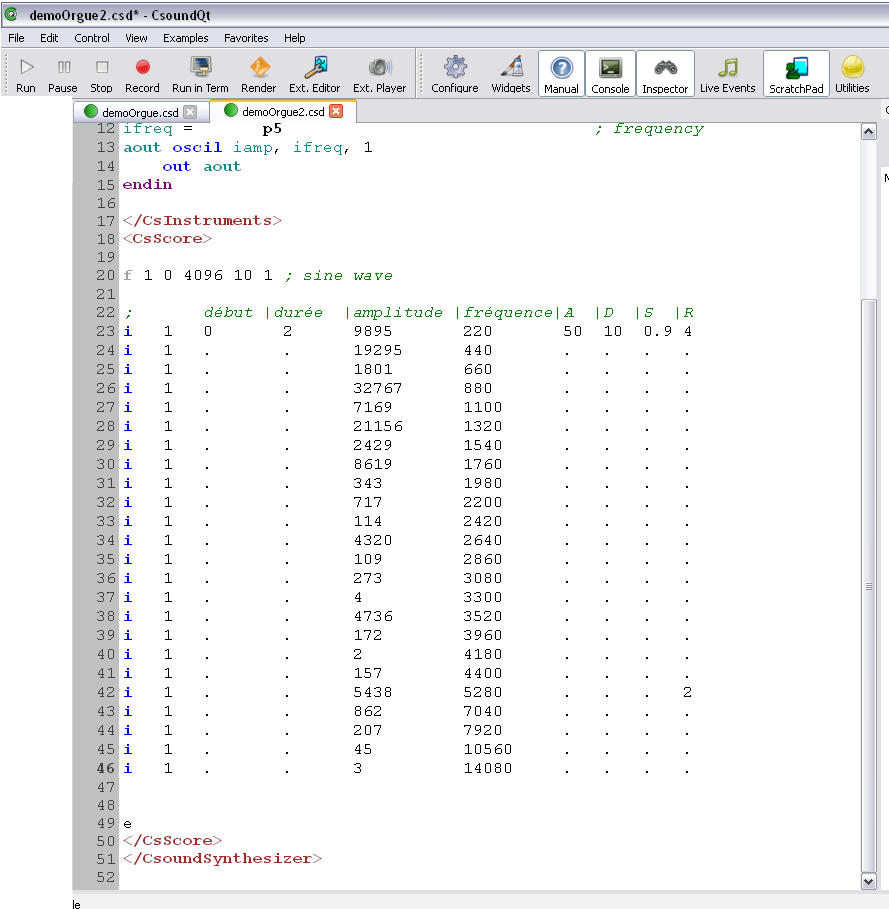
À chaque ligne correspond une sinusoïde, caractérisée par :
- sa durée (en seconde)
- son amplitude (de 1 à 32 767)
- la durée de son attaque (ici, 50 signifie que l'attaque occupe un cinquantième de la durée totale de la note)
- la durée de son déclin (10 signifie un dixième de la durée totale)
- l'amplitude de son soutien (comprise entre 0 et 1) par rapport à son amplitude maximale
- et la durée de son relâchement (exprimée, comme pour l'attaque, en fraction de la durée totale). Le relâchement dure un quart de la note pour les amplitudes inférieurs, et une moitié pour les harmoniques de fréquence supérieure à 5 000Hz (le point signifie que la valeur est identique à celle située juste au-dessus). On avait remarqué que les harmoniques les plus aigus s'éteignaient plus vite que les harmoniques inférieurs. Ce qui nous donne :

Ensuite, on peut facilement retrouver les fréquences des autres notes (voir encadré déroulant) du morceau, et les agencer grâce à Csound :

Quand physique rime avec musique

Dans la musique occidentale, il existe 12 notes de musique : Do, Do#, Ré, Ré#, Mi, Fa, Fa#, Sol, Sol#, La, La# et Si. Et comme il existe bien sûr plus de 12 hauteurs de notes différentes, cette série se répète donc. On repère donc les notes avec leur nom et le numéro de leur série. Par exemple, le La3 est le La de la 3ème série, celui du diapason, le fameux La 440Hz.
La portée ci-dessous représente cette troisième série (en rouge, le La3) :

Cliquer sur l'image pour agrandir

L'intervalle entre deux notes de même nom de deux séries consécutives (par exemple entre un Do3 et un Do4) s'appelle l'octave. Et cette octave se divise elle-même en douze demi-tons, qui forment la gamme chromatique. Mais pourquoi douze ? À quelle réalité physique correspond ce système ?
En fait, l'octave correspond à l'intervalle entre une note et une note qui fait le double de sa fréquence. Ainsi, le La2 a pour fréquence 220Hz, et le La4 880Hz. Donc, puisque l'octave correspond à une multiplication de la fréquence par 2, chaque demi-ton (douzième d'octave) correspond à une multiplication par 2^1/12. À partir du La3, on peut retrouver facilement les fréquences des autres notes :

L'intérêt de cette division de l'octave en 12 ? Il apparaît quand on compare les harmoniques d'une note avec les autres notes de la gamme :

On constate que les harmoniques ont tous des fréquences très proches d'autres notes de la gamme, voire même égales (pour les La). Notre système occidental n'est donc pas arbitraire : c'est un moyen de rapprocher au maximum la musique (les fréquences des notes) de la réalité physique du son (les fréquences harmoniques). Et c'est pourquoi les accords parfaits majeurs (comme l'accord de La Majeur : La-Do#-Mi, contrôleur audio ci-dessous) sont si mélodieux : les notes les composant ont des harmoniques communs.

Bien sûr, on est encore loin d'un mimétisme vraiment convaincant. Pour améliorer notre son, il faudrait tenir compte du bruit (toutes les fréquences qui ne sont pas amplifiées par les tuyaux de l'orgue parce qu'elles ne correspondent à aucun harmonique, mais qui jouent cependant un rôle dans le timbre), définir une enveloppe plus précise en jouant sur les ondulations du son...

Cependant, même la synthèse la plus précise ne peut reproduire parfaitement la nature. Aucun ordinateur ne peut reproduire toutes les petites imperfections, volontaires ou involontaires, que commettent les vrais instrumentistes, et qui font la musique...

Caractéristiques d'un son

Conclusion