Caractéristiques d'un son
C'est évident pour tout le monde : une guitare n'a pas le même son qu'une flûte. Mais où se situe exactement la différence ?
Bien sûr, tout le monde est capable de reconnaître le son d’une flûte de celui d’une guitare, mais ce n'est pas tout : imaginons une guitare et une flûte jouant la même note, un do par exemple. La hauteur est la même, mais les sons sont parfaitement différenciables.
Dans un premier temps, nous nous intéresserons aux caractéristiques du son. Ensuite nous verrons comment celles-ci confèrent aux instruments leurs sonorités différentes, leurs "couleurs" ; enfin, à l'aide d'un logiciel informatique, nous reproduirons un son, que nous aurons choisi au préalable.
a) Fréquence
Le son étant un phénomène périodique, on peut calculer l'inverse de sa période, c'est-à-dire sa fréquence (exprimée en Hertz). Mais quelle influence a cette fréquence sur le son ? Pour le savoir, écoutons les sons ci-dessous :



On constate que, lorsque la période de la courbe diminue, c'est-à-dire que sa fréquence augmente, le son devient plus aigu.
Pour les humains, le spectre audible s'étend de 20Hz à 20 000Hz – intervalle variant selon les individus et diminuant avec l'âge.
b) Intensité
L'intensité ou volume est le paramètre du son le plus instinctif : il fait que l'on dit qu'un son est "fort" ou "ténu".
D'un point de vue physique, l'intensité d'un son est la puissance par unité de surface transportée par une onde sonore (exprimée en Watt par mètre carré). En pratique, mesurer cette puissance en W.m-2 s'avère plutôt difficile, car un microphone ne fournit comme information, on l'a dit, qu'un courant à tension variable. Cependant le microphone peut nous aider à comprendre quelle caractéristique de l'onde sonore détermine son intensité.
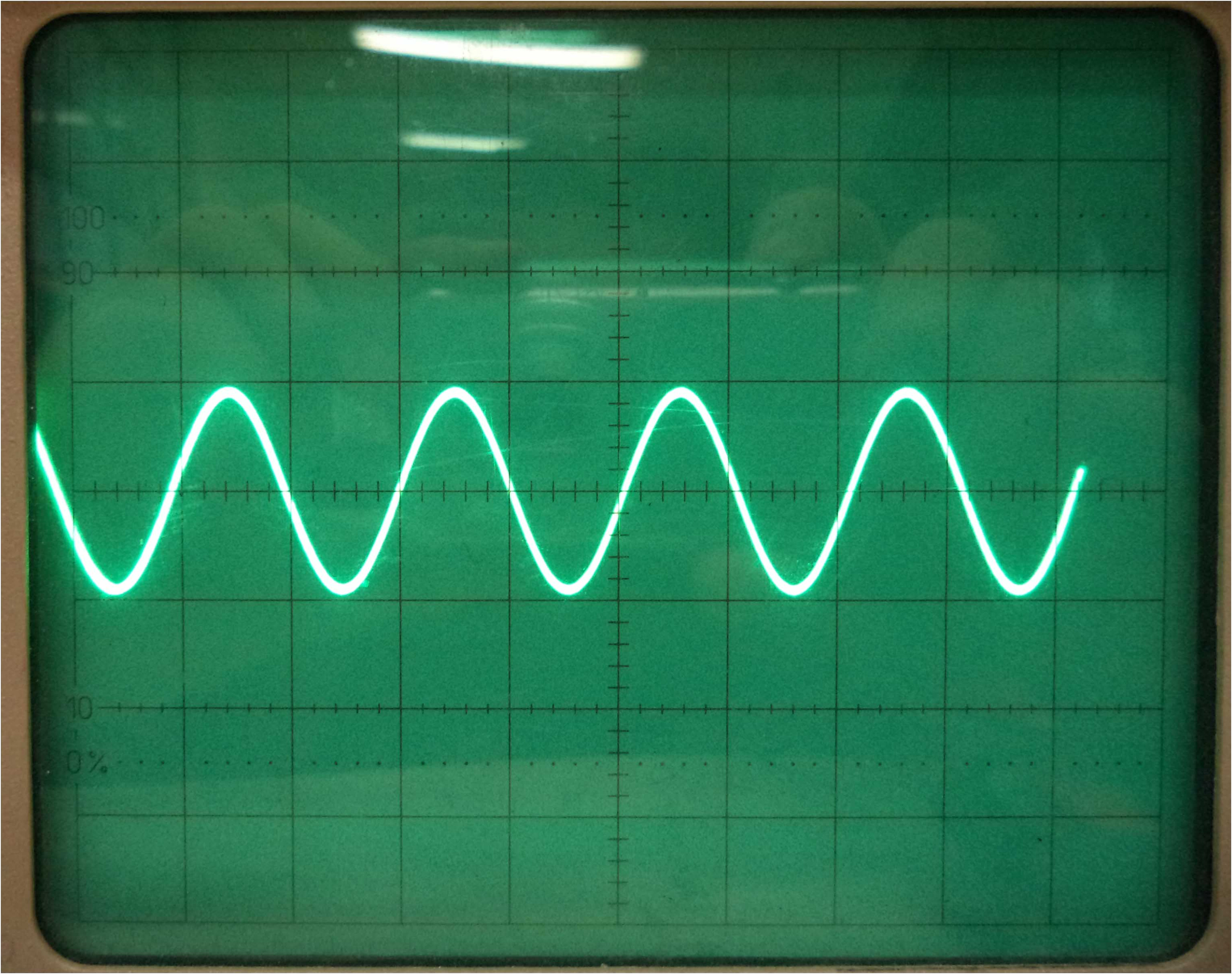
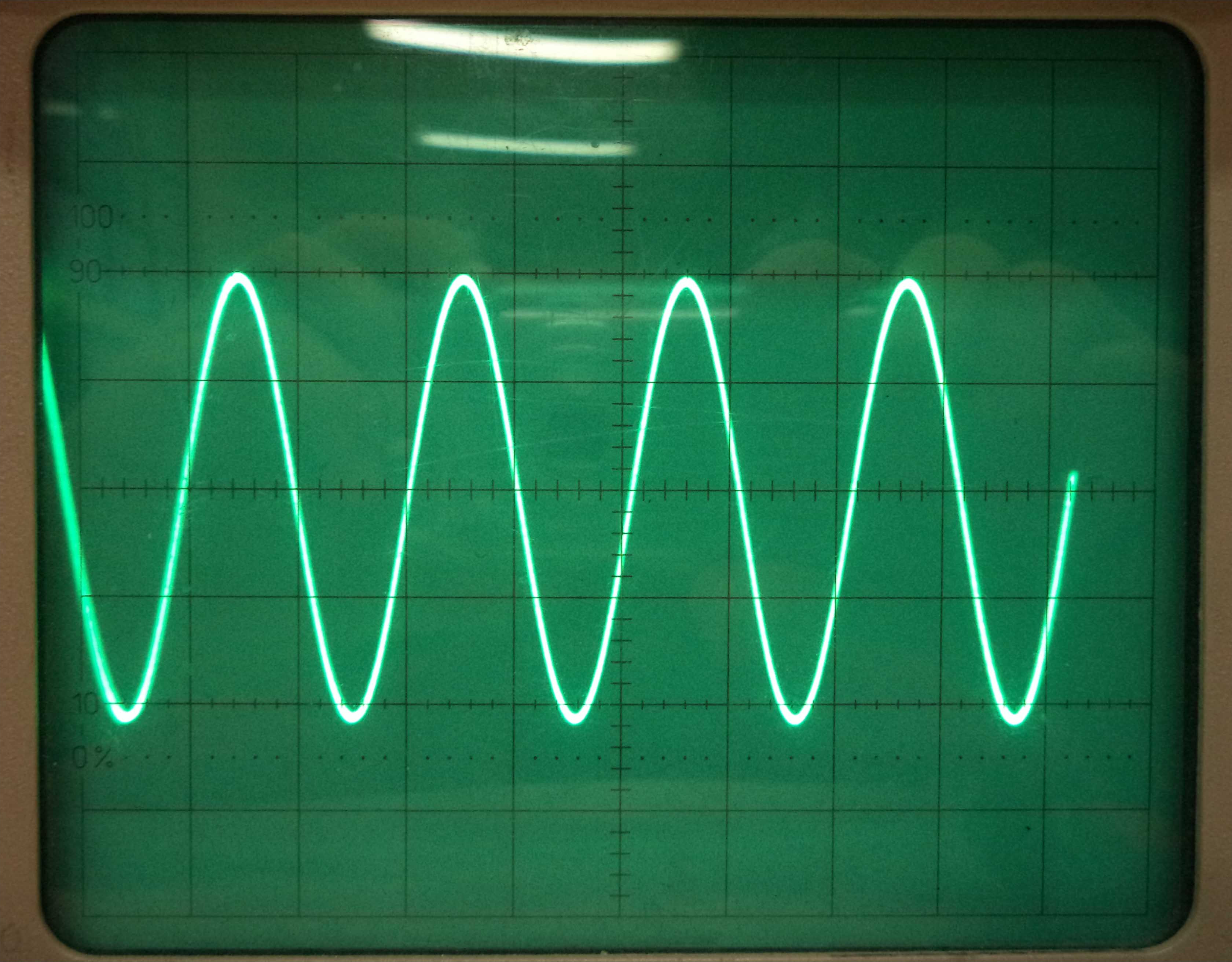
On constate que les deux sinusoïdes sont exactement identiques, à l'exception de la "hauteur des bosses", de l'amplitude des vibrations. Cela signifie que les variations de tension du courant généré par le microphone sont plus importantes, c'est-à-dire que les déplacements de la membrane sont plus amples. Au niveau de l'onde sonore, cela s'explique par le fait que les différences de pression entre les zones de surpression et les zones de dépression sont plus importantes.
L'intensité d'un son est donc la différence de pression entre les "creux" et les "bosses" de l'onde sonore.
Tout le monde sait qu'un son n'est pas infini, il a un cycle de vie. L’évolution globale de l’intensité d’un son dans le temps s’appelle l'enveloppe sonore, et peut être décomposée en quatre parties :

- L'attaque — Attack en anglais — du son correspond au temps que met le son pour atteindre son intensité maximale,
- Le déclin — Decay — fait la transition entre l'attaque et la phase de maintien,
- Le maintien — Sustain — est le corps de la note, la phase où le son est maintenu,
- Le relâchement — Release — caractérise la vitesse à laquelle l'intensité diminue avant que le son s'éteigne.
Ainsi, on a coutume d'appeler l'enveloppe sonore l'enveloppe ADSR.
c) Timbre
Le timbre d'un son est sa "couleur" propre, ce qui fait que deux notes de même intensité et de même fréquence jouées par deux instruments différents sont distinguables. Dans cette partie, nous verrons quelles sont les caractéristiques de l'onde sonore qui déterminent ce fameux timbre.
Jusqu'ici, nous ne nous sommes intéressés qu'à des sons purs, et, bien qu'ils soient fascinants, ils peuvent - à force d'être écoutés - susciter d'importants maux de tête...

Reconnaissons que la même note jouée à l'orgue est beaucoup plus agréable !
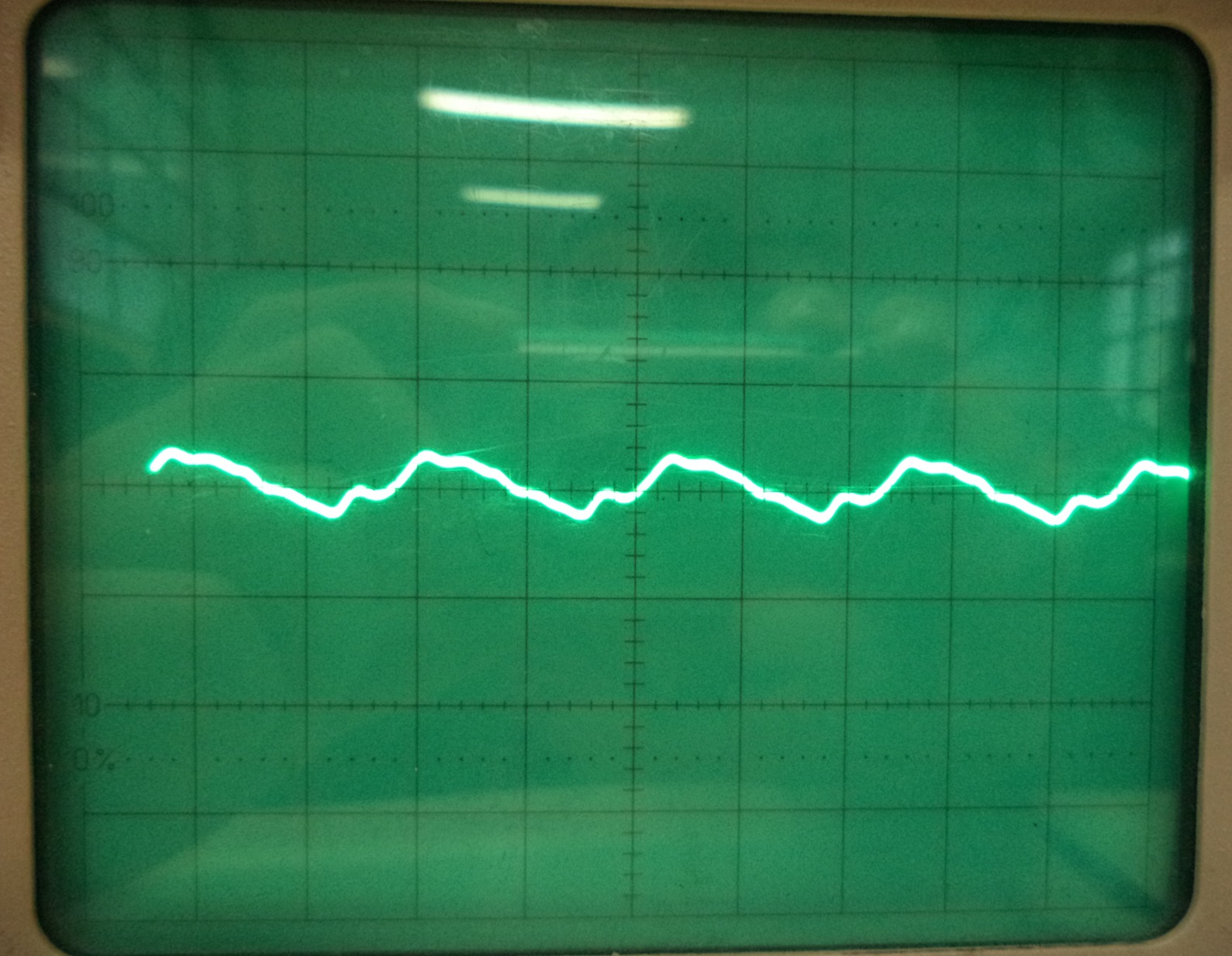
Mais alors, puisqu'on a la même fréquence et la même intensité, où donc se situe la différence ?
- Fondamentale et harmoniques
Quand un corps vibre, nous l'avons vu, il produit un son. Mais ce son n'est jamais un son pur. Et, par ailleurs, un même corps peut produire, sans aucun changement dans sa structure, de nombreux sons différents, à des fréquences différentes. Voici par exemple une flûte traversière dont toutes les clés (trous) sont bouchées :
Juste en soufflant de plus en plus fort, on peut obtenir tous ces sons, avec exactement les mêmes caractéristiques du corps vibrant. Comment est-ce possible ?
Il nous faut d'abord comprendre ce qu'il se passe lorsqu'un corps « entre en résonance », c'est-à-dire lorsqu'il se met à produire un son audible avec une certaine fréquence.
Pour cela, prenons l'exemple d'une corde. Si on la fait vibrer (en la pinçant, en la frappant, en la frottant avec un archet...), des ondes vont naître et se propager le long de la corde, à partir du point où on l'a excitée. Ces ondes vont ensuite rebondir sur les extrémités de la corde, et puis, dans la plupart des cas, mourir lentement à cause de la perte d'énergie due aux frottements. Cependant, il se peut aussi que les ondes qui rebondissent se superposent parfaitement avec celles allant dans l'autre sens. Dans ce cas, les ondes vont peu à peu s'amplifier, jusqu'à acquérir tellement d'énergie que l'air déplacé par la corde nous transmette un son audible : le système est entré en résonance.
Un petit schéma peut sans doute nous aider à mieux comprendre. L'animation ci-dessous représente une portion de corde fixée aux deux extrémités. Les ondes partant du point d'excitation (à gauche, en dehors de l'image) sont représentées en bleu ; celles ayant rebondi et revenant le long de la corde dans l'autre sens, en rouge. En noir, on a la somme des deux ondes : la vibration effective de la corde (au ralenti).
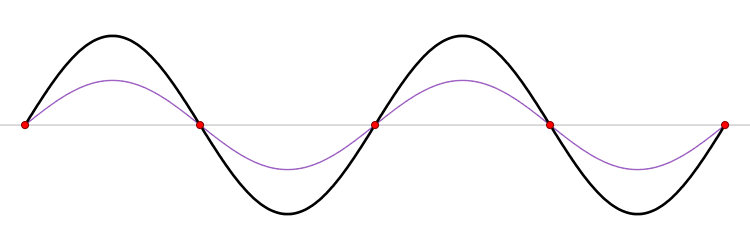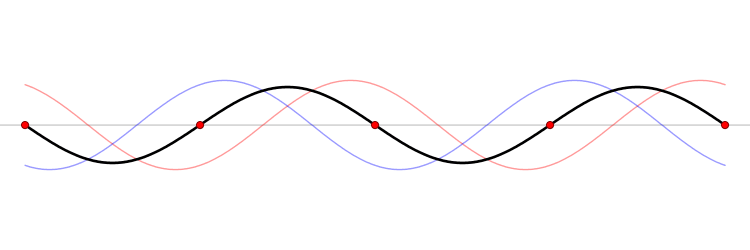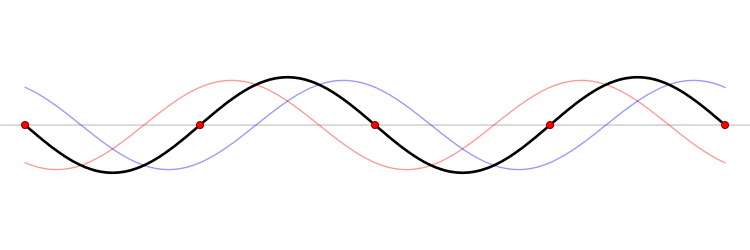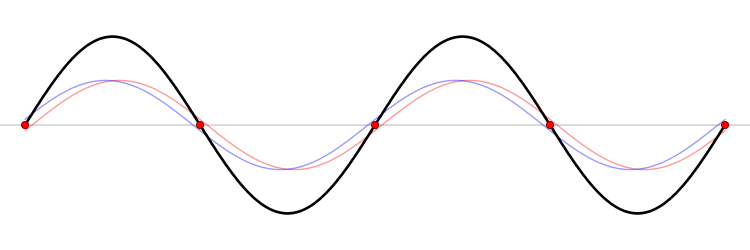
— Wikimedia Commons
Pour chaque corde, ce phénomène n'est possible que pour une certaine longueur d'onde (autrement les ondes bleues et rouges ne se superposeraient pas parfaitement). Cette longueur d'onde "parfaite" dépend de la longueur de la corde, mais aussi de la vitesse de propagation des ondes, déterminée par sa densité, sa tension... Ainsi un système acoustique filtre pour ainsi dire toutes les fréquences, pour ne garder et n'amplifier que sa fréquence de résonance.
Mais le plus beau du plus beau, c'est que là où on peut mettre un ventre, on peut en mettre deux, de longueur deux fois plus petite ! L'expérience dite de la corde de Melde permet de visualiser particulièrement bien le phénomène. On a une corde de longueur et de tension fixes, excitée à une extrémité par un vibreur vertical à fréquence variable. Ainsi, à une fréquence f, la corde entre en vibration pour former un ventre unique. C'est donc la fréquence la plus basse pour laquelle une onde stationnaire apparaît dans le système, appelée fréquence fondamentale. Puis, à une fréquence 2f, la corde entre de nouveau en résonance pour former deux ventres. À une fréquence 3f, trois ventres, etc... Les fréquences 2f, 3f, 4f... c'est-à-dire les multiples entiers (naturels) de la fréquence fondamentale sont appelées harmoniques 1, 2, 3, 4... du fondamental.
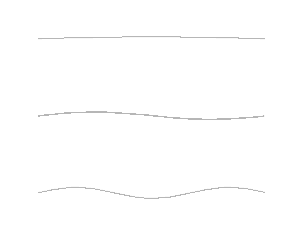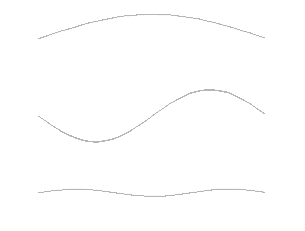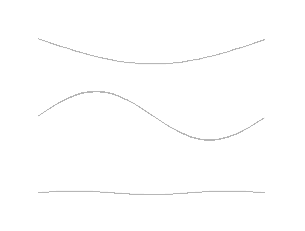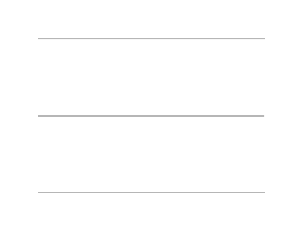
— Wikimedia Commons
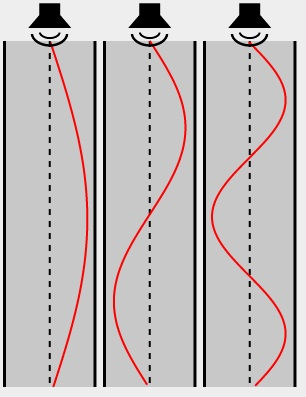
— Wikimedia Commons
Maintenant, on peut comprendre parfaitement ce qui se passe dans la flûte traversière. Dès la première note, tous les harmoniques étaient présents dans le son. Puis, suivant la façon dont on souffle dans la flûte, leurs intensités relatives varient. En fait, l'oreille attribue à un son la fréquence de l'harmonique dont l'intensité est la plus importante.
On peut revenir sur la formule mentionnée dans le b) Périodicité. Si la sinusoïde d'une fondamentale a pour équation y = sin(t), celle de son harmonique 2 est y = sin(2t), celle de son harmonique 3, y = sin(3t), etc... Et la somme serait : y = sin(t) + sin(2t) + sin(3t) + sin(4t)...
En fait, c'est un peu plus complexe que ça. Il faut aussi prendre en compte les intensités relatives des différents harmoniques, lesquelles varient aussi suivant les corps vibrants et la façon dont on les excite. La formule exacte serait ainsi y = a*sin(t) + b*sin(2t) + c*sin(3t)...
Maintenant qu'on sait ça, on peut commencer à synthétiser des sons de fréquence et d'intensité fixes, mais dont les harmoniques et leurs intensités relatives varient (nous avons utilisé le logiciel Harmonie) :
Dans les trois cas, il s'agit d'un la 440Hz, cependant on entend bien que ces sons sont différents. Bien sûr, on est encore loin de la reproduction fidèle d'un instrument, mais on s'en approche lentement (avec beaucoup d'imagination, le deuxième ressemble vaguement à une cornemuse, non ?)...
- Enveloppe sonore
Cependant, le timbre d’un son ne dépend pas que de ses harmoniques à un instant donné. Pour s’en convaincre, écoutons ce son, correspondant à l’enregistrement d’une note, et inversée dans le temps, c’est à dire "jouée à l'envers".
Voici maintenant le son original, joué à l’endroit :
Dans le bon sens, c’est tout de suite plus facile à reconnaître, non ? L’enveloppe ADSR et ses quatre lettres sont donc un facteur clef du timbre.
Dans le cas d'une percussion ou d'une corde pincée, l'attaque est très rapide, le maintien inexistant et le relâchement très long. Dans le cas d'un instrument à vent, l'attaque est plus lente, le soutien beaucoup plus long et peut être modifié par le musicien, et le relâchement est relativement court.

- Evolution des harmoniques dans le temps
Un dernier petit paramètre est à prendre en compte, mélange des deux précédents : l'évolution dans le temps des intensités relatives des différents harmoniques.
Le meilleur exemple pour illustrer cela est sans doute celui d'une cloche : au moment de l'impact entre le battant et le corps de la cloche, on entend fortement une certaine note. Puis, pendant que le son retentit, d'autres harmoniques (plus aigus) gagnent en puissance et apparaissent :



